[NumPy]正規化（Normalization）を行う

正規化とはデータを扱いやすいスケールに変更する手法です。ここでは代表的なMin-Max normalization、Z-score normalizationについて解説します。

• Min-Max normalization
• Z-score normalization

Min-Max normalization

正規化というとMin-Max normalizationを指すといわれることもありますが、正直そこまで気にする必要はありません。どちらかというと、正規化を行うときにデータの性質に応じて適切な手法を選択できる方が重要です。

Min-Max normalizationとは

Min-Max normalizationとは、データを最小値0、最大値1にスケールする手法です。

データ$x_i$をMin-Max normalizationで正規化した$x^{\prime}_i$は以下の式で求めます。

$$ x^{\prime}_i = \frac{x_i – min(x)}{max(x) – min(x)} \quad (i = 1, 2, \cdots , n) $$

Min-Max normalizationは外れ値に弱いという特徴があります。最小値と最大値がはっきりしている場合に適した手法です。外れ値が含まれる場合は後述のZ-score normalizationを使用する方が適しています。

NumPyによる実装

では、実際にNumPyで実装してみましょう。

まずは、正規化前の5×5の行列を作成します。再現しやすいように乱数のシードは固定しておきます。

np.random.seed(123)
x = np.random.random((5, 5))
print(x)
[[0.69646919 0.28613933 0.22685145 0.55131477 0.71946897]
 [0.42310646 0.9807642  0.68482974 0.4809319  0.39211752]
 [0.34317802 0.72904971 0.43857224 0.0596779  0.39804426]
 [0.73799541 0.18249173 0.17545176 0.53155137 0.53182759]
 [0.63440096 0.84943179 0.72445532 0.61102351 0.72244338]]

正規化前後でどう変わったかわかりやすいように最小値、最大値、平均値、標準偏差を求めておきます。

print('最小値　：%f' % np.min(x))
print('最大値　：%f' % np.max(x))
print('平均値　：%f' % np.mean(x))
print('標準偏差：%f' % np.std(x))
最小値　：0.059678
最大値　：0.980764
平均値　：0.524464
標準偏差：0.226296

式の定義どおりに実装します。np.min関数で最小値、np.max関数で最大値を求めています。

x_norm = (x - np.min(x)) / (np.max(x) - np.min(x))
print(x_norm)
[[0.02615693 0.72523256 0.32482616 0.41610292 0.11393134]
 [[0.69134813 0.24586343 0.18149608 0.53375766 0.71631841]
 [0.39456516 1.         0.67871147 0.45734477 0.36092125]
 [0.30778888 0.72671997 0.41135597 0.         0.36735576]
 [0.73643209 0.13333586 0.12569274 0.51230105 0.51260093]
 [0.62396223 0.85741574 0.72173197 0.59858193 0.71954765]]

ぱっと見で最小値0、最大値1であることはわかりますが、念のため先ほどと同じように最小値、最大値、平均値、標準偏差を確認しましょう。

print('最小値　：%f' % np.min(x_norm))
print('最大値　：%f' % np.max(x_norm))
print('平均値　：%f' % np.mean(x_norm))
print('標準偏差：%f' % np.std(x_norm))
最小値　：0.000000
最大値　：1.000000
平均値　：0.504606
標準偏差：0.245684

最小値0、最大値1であることが確認できます。加えて、若干値が違いますが、平均値と標準偏差はほとんど変わっていないことがわかります。

最小値0、最大値1にスケールする仕組みを理解する

Z-score normalizationは平均0、標準偏差1にスケールする手法になります。

わかりやすいデータを使って計算過程をひとつずつ確認して、最小値0、最大値1の範囲にスケールする仕組みを確認していきましょう。

まずは、以下のようなデータを用意します。10、20、・・・、50と10ずつ増える5個のデータです。

x = np.array([10, 20, 30, 40, 50])
print(x)
[10 20 30 40 50]

まずは分子から確認します。データから最小値を引きます。最小値は10なので、各要素から引くと以下のようになります。

print(x - np.min(x))
[ 0 10 20 30 40]

次に分母を見てみます。最大値50から最小値10を引くので、40になります。

print(np.max(x) - np.min(x))
40

すでに計算した分子の最大値は40で、分母と同じ値ですので、割り算の結果は1になります。一方で、最小値は0ですので、割り算の結果は0になります。それ以外の値は最小値と最大値の間に収まるため、計算結果はすべて0以上1以下になります。

print((x - np.min(x)) / (np.max(x) - np.min(x)))
[0.   0.25 0.5  0.75 1.  ]

Z-score normalization

次にZ-score normalizationについて確認します。標準化（Standardization）とも呼ばれることもありますが、こちらもそれほど気にする必要はありません。

Z-score normalizationとは

データ$x_i$をZ-score normalizationで正規化した$x^{\prime}_i$は以下の式で求めます。

$$ x^{\prime}_i = \frac{x_i – \bar{x}}{\sigma} \quad (i = 1, 2, \cdots , n) $$

NumPyによる実装

正規化前のデータおよび最小値、最大値、平均値、標準偏差を再掲しておきます。

np.random.seed(123)
x = np.random.random((5, 5))
print(x)
[[0.69646919 0.28613933 0.22685145 0.55131477 0.71946897]
 [0.42310646 0.9807642  0.68482974 0.4809319  0.39211752]
 [0.34317802 0.72904971 0.43857224 0.0596779  0.39804426]
 [0.73799541 0.18249173 0.17545176 0.53155137 0.53182759]
 [0.63440096 0.84943179 0.72445532 0.61102351 0.72244338]]

print('最小値　：%f' % np.min(x))
print('最大値　：%f' % np.max(x))
print('平均値　：%f' % np.mean(x))
print('標準偏差：%f' % np.std(x))
最小値　：0.059678
最大値　：0.980764
平均値　：0.524464
標準偏差：0.226296

こちらも同様に式どおりに実装します。np.mean関数が平均（算術平均）、np.std関数が標準偏差を求める関数です。

x_norm = (x - np.mean(x)) / np.std(x)
print(x_norm)
[[ 0.76008999 -1.05315055 -1.31514268  0.11865512  0.86172564]
 [-0.44789519  2.01638476  0.70865548 -0.19236556 -0.58483479]
 [-0.8010976   0.90406276 -0.37955215 -2.05387975 -0.55864464]
 [ 0.94359364 -1.51116753 -1.54227706  0.03132102  0.0325416 ]
 [ 0.48581156  1.43602912  0.88376026  0.38250702  0.87486952]]

正規化後の最小値、最大値、平均値、標準偏差を見てみましょう。

print('最小値　：%f' % np.min(x_norm))
print('最大値　：%f' % np.max(x_norm))
print('平均値　：%f' % np.mean(x_norm))
print('標準偏差：%f' % np.std(x_norm))
最小値　：-2.053880
最大値　：2.016385
平均値　：-0.000000
標準偏差：1.000000

平均値0、標準偏差1にスケールされていることがわかります。また、最小値と最大値も変わっていることにも注意してください。

平均値0、標準偏差1にスケールする仕組みを理解する

Z-scoreについても平均値0、標準偏差1にスケール仕組みをひとつずつ確認していきましょう。

データは先ほどと同じデータを使います。

x = np.array([10, 20, 30, 40, 50])
print(x)
[10 20 30 40 50]

このデータの平均は30、標準偏差は$\sqrt{200}$になります。

print('平均値　：%f' % np.mean(x))
print('標準偏差：%f' % np.std(x))
平均値　：30.000000
標準偏差：14.142136

まずは分子から見ていきます。平均値30を引くので、分子の平均値は0になります。同様に標準偏差求めると$\sqrt{200}$になっています。

print('平均値　：%f' % (x - np.mean(x)).mean())
print('標準偏差：%f' % (x - np.mean(x)).std())
平均値　：0.000000
標準偏差：14.142136

分母は分子の標準偏差と同じ$\sqrt{200}$でしたので、割った結果の標準偏差は1になります。

print((x - np.mean(x)) / np.std(x))
[-1.41421356 -0.70710678  0.          0.70710678  1.41421356]

実際に平均値と標準偏差を求めます。

print('平均値　：%f' % np.mean((x - np.mean(x)) / np.std(x)))
print('標準偏差：%f' % np.std((x - np.mean(x)) / np.std(x)))
平均値　：0.000000
標準偏差：1.000000

外れ値に弱いとはどういうことか

Min-Max normalizationは外れ値に弱いという説明をしました。これがどういうことか、Z-score normalizationなら大丈夫なのかについて具体的な例を使って確認します。

以下のような具体例を用意します。

1,000人分の身長データを使って正規化を行います。身長データは正規分布に従いますが、990件は正常データで10件は外れ値であるとします。
この外れ値は100の位の1が読み取れず欠損したデータ（180cmが80cmになってしまった）が10件あるとします。

まずは必要なパッケージをインポートします。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

正常データを作成する

まずは正常データ990件を用意します。それっぽい身長データにするために、平均値170、標準偏差10の正規分布に従う乱数を生成します。

np.random.seed(123)
x = np.random.normal(loc=170, scale=10, size=990)

これをヒストグラムで描画してみます。

plt.hist(x, bins=100)
plt.show()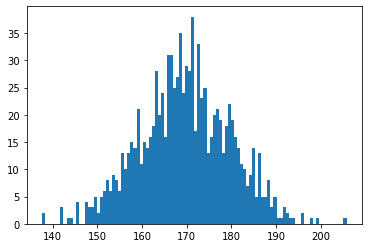

numpy.random.normal関数を使って作成したデータですので正規分布に従っています。

ではこのデータをMin-Max normalization、Z-score normalizationで正規化し、同様にグラフを出力してみましょう。

正常データをMin-Max normalizationで正規化する

まずはMin-Max normalizationを使って正規化します。

x_norm = (x - np.min(x)) / (np.max(x) - np.min(x))
plt.hist(x_norm, bins=100)
plt.show()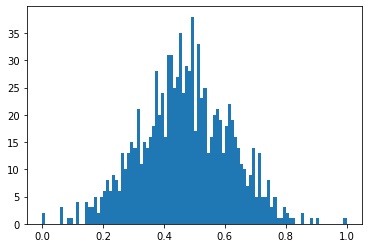

最小値0、最大値1にスケールしただけで分布は変わっていません。

正常データをZ-score normalizationで正規化する

次にZ-score normalizationを使って正規化してみます。

x_norm = (x - np.mean(x)) / np.std(x)
plt.hist(x_norm, bins=100)
plt.show()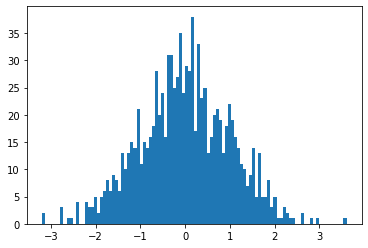

こちらも中心が0になっているだけで、分布は変わっていません。

外れ値を生成して正常データに加える

では、外れ値を10件生成し、それを正常データに加えていきます。

e1 = np.random.normal(loc=170, scale=10, size=10)-100
print(e1)
[60.91733437 76.55533937 72.40244965 63.547099   73.60026527 51.22368305
 72.34040489 76.24323922 78.11939825 49.77843013]

外れ値は単純に100を引いた値を使います。

このデータを正常値に加え、念のためシャッフルしておきます。

x2 = np.concatenate([x, e1])
np.random.shuffle(x2)
plt.hist(x2, bins=100)
plt.show()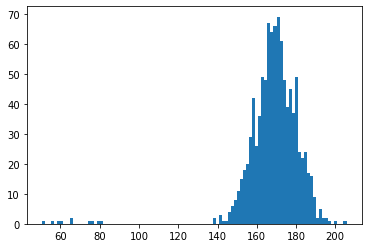

外れ値は小さい値を用意したため、グラフは右に寄った形になっています。

では、これをMin-Max normalization、Z-score normalizationで正規化してみます。

外れ値を含むデータをMin-Max normalizationで正規化する

先ほどと同様の手順で正規化してグラフを出力します。

x2_norm = (x2 - np.min(x2)) / (np.max(x2) - np.min(x2))
plt.hist(x2_norm, bins=100)
plt.show()

外れ値を含まない場合は0.2から0.8くらいの範囲にデータが分布していましたが、外れ値を含むと0.6から0.9くらいの範囲に分布していることがわかります。
もともとは0.5くらいが中心でしたが、0.7から0.8あたりに中心が来ており、データが偏っていることになります。

これが外れ値に弱い（外れ値に敏感ともいう）ということになります。

外れ値を含むデータをZ-score normalizationで正規化する

では、Z-score normalizationだとどうなるでしょうか。

x2_norm = (x2 - np.mean(x2)) / np.std(x2)
plt.hist(x2_norm, bins=100)
plt.show()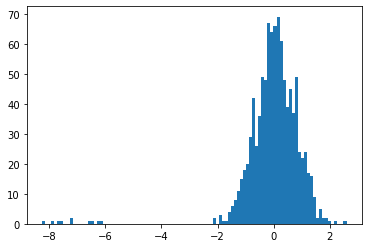

こちらもグラフ自体は偏っていますが、外れ値を含まない場合も外れ値を含む場合も-2から2の範囲に分布していることがわかります。
外れ値を含んでいますが、正規化後の分布はほとんど変わっていない、すなわち外れ値に強いということがいえます。

このことから外れ値を含む場合や外れ値を除外できない場合は、Min-Max normalizationよりもZ-score normalizationの方が適しているといえます。
ただし、外れ値のデータを除外したり、外れ値を修正・補完して、想定される最小値・最大値の範囲できるのであれば、Min-Max normalizationを使用して正規化することも可能であることも覚えておいてください。